※このページではデータ構造のサンプルコードを記載していますが、基本・応用情報技術者試験の合格だけなら見る必要はありません。
データ構造とはなにか?
プログラミング未経験の方は、「データ構造」と聞いても何がなんだかわからないと思うので、はじめにざっくりと説明します。
プログラミングは、変数と呼ばれる箱にデータを入れ、箱の中身に変更を加えていくことで様々な処理が行えるようになっています。
int x = 1; //整数専用のxという箱に1を入れる
int y = 3; //整数専用のyという箱に3を入れる
int z = x + y; //zという箱にxとyを足した数(4)を入れる
z = z * z; //zという箱にzとzをかけた数(4×4=16)を再代入するこのように、1つの箱に対して1つのデータが入るのならば単純なのですが、1つの箱に対して複数のデータを入れたいケースが出てきます。
このとき、データの入れ方、もしくは箱の構造をよく考えないと、データを取り出したり計算したりするときに時間がかかってしまいます。そのため、複数のデータを効率的に扱いやすく管理できる箱の構造を学ぶ必要があるのです。
様々なデータ構造
・変数を宣言したとき、メモリ空間に領域が確保されます。
・変数のデータが格納されているメモリ空間の位置を「ポインタ」と言います。
配列
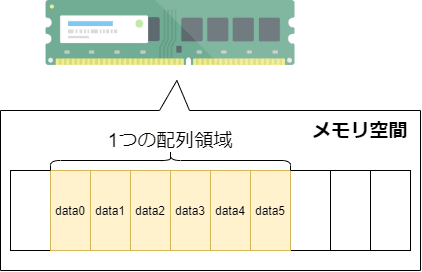
配列は、固定長のメモリ領域が連続して並んでいる単純な作りになっており、データを順番に格納することができます。データの順番を示す番号をインデックスと言います。
プログラミングで間違えられやすいのは、インデックスは0から始まるため、3番目のデータを指定したい場合はインデックス番号に2を指定する必要がある、ということです。
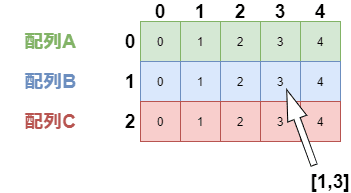
また、配列の中に配列を入れるような、二重構造にすることができます。このような配列を2次元配列と言います。
【C】配列の値とアドレスを表示するサンプル
コーディングできるようになる必要はありませんが、参考程度にサンプルコードを貼っておきます。要素数が10個のint配列を作成し、値とアドレスを表示するサンプルとなっています。アドレスが同じなので、同じ領域に変数が存在することがわかります。
#include <stdio.h>
#include <string.h>
int main(void)
{
int array[] = { 10, 20, 30, 40, 50, 60, 70, 80, 90, 100 };
for (int i = 0; i < 10; i++) {
int data = array[i];
int* p = &data;
printf("index%d:データ%d アドレス%p\n",i,array[i],p);
}
}
// index0:データ10 アドレス00AFFAF0
// index1:データ20 アドレス00AFFAF0
// index2:データ30 アドレス00AFFAF0
// index3:データ40 アドレス00AFFAF0
// index4:データ50 アドレス00AFFAF0
// index5:データ60 アドレス00AFFAF0
// index6:データ70 アドレス00AFFAF0
// index7:データ80 アドレス00AFFAF0
// index8:データ90 アドレス00AFFAF0
// index9:データ100 アドレス00AFFAF0リスト
リストは、メモリ領域上に点在するデータをポインタで繋ぎ合わせたデータ型です。配列と違い、メモリ上に連続した領域を確保しなくて良いのが特徴です。
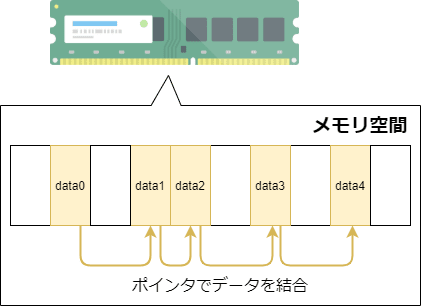
ポインタを変更することで、データの追加、挿入、削除を柔軟に行えるのが特徴です。
新しいデータのポインタを指定することでデータの挿入ができたり、一つ飛ばしたデータのポインタを指定することでデータの削除ができたりします。
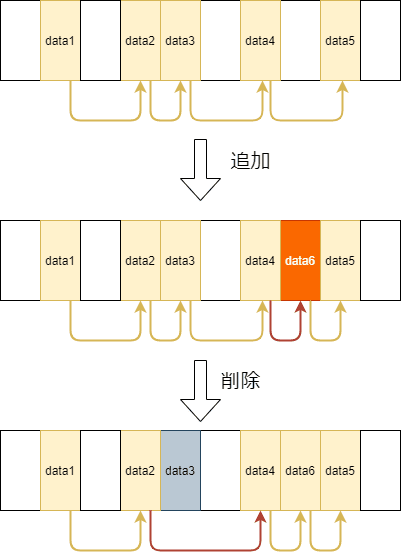
また、リストはポインタの持ち方が3種類あり、
・次のデータへのポインタを持つ単方向リスト(線形リスト)
・次のデータと前のデータへのポインタを持つ双方向リスト
・最後のデータが最初のデータのポインタを持つ環状リスト
に分けることができます。
【C】単方向リストのアドレスを表示するサンプル
5つの構造体型変数からなるリストを作成し、それぞれのアドレスを表示するサンプルを作ってみました。配列と違い、各変数の保存領域が異なりますから、アドレスがすべて別のものになっていることが特徴です。
#include <stdio.h>
#include <string.h>
typedef struct item
{
int num; //アイテムの番号
struct item* next; //次の要素のアドレス
} ITEM;
int main(void)
{
// 変数定義
ITEM item1;
ITEM item2;
ITEM item3;
ITEM item4;
ITEM item5;
// アイテム番号と次の要素のアドレスをセット
item1.num = 1;
item1.next = &item2;
item2.num = 2;
item2.next = &item3;
item3.num = 3;
item3.next = &item4;
item4.num = 4;
item4.next = &item5;
item5.num = 5;
item5.next = NULL;
// 現在のアイテムを1つめにセット
ITEM* currentItem = &item1;
while (1) {
printf("データ%d 自分のアドレス%p 次のアドレス%p \n", currentItem->num, currentItem, currentItem->next);
// 次の要素のアドレスがNULL
if (!currentItem->next) {
break;
}
// 現在のアイテムを次の要素にセット
currentItem = currentItem->next;
}
}
// データ1 自分のアドレス00FDF84C 次のアドレス00FDF83C
// データ2 自分のアドレス00FDF83C 次のアドレス00FDF82C
// データ3 自分のアドレス00FDF82C 次のアドレス00FDF81C
// データ4 自分のアドレス00FDF81C 次のアドレス00FDF80C
// データ5 自分のアドレス00FDF80C 次のアドレス00000000キュー
キューは、最初に入れたデータから取り出せるデータ構造です。筒に、入れたものを逆から取り出す、というイメージを持つとわかりやすいでしょう。
キューにデータを入れる操作をエンキュー(enqueue)、取り出す操作をデキュー(dequeue)と言います。
「データ1、データ2、データ3、データ4」という順番で入れたなら、取り出せる順番は同様に「データ1、データ2、データ3、データ4」となります。データ4から取り出すことはできません。

このように、最初に入れたものから取り出すという構造を先入れ先出し方式といい、英語だと「First-In First-Out(FIFO)」とも言います。
【C#】キュー型のデータにエンキュー・デキューするサンプル
C#では、複数のオブジェクトをキューとして管理するコレクションが用意されています。実際にエンキュー・デキューを行ってみます。格納した順に取り出せていることがわかります。一度取り出したものはキューには残りません。
var queue = new Queue<string>();
queue.Enqueue("あ");
queue.Enqueue("い");
queue.Enqueue("う");
queue.Enqueue("え");
queue.Enqueue("お");
while (queue.Count > 0)
{
Console.WriteLine(queue.Dequeue());
}
//あ
//い
//う
//え
//おスタック
スタックは、最後に入れたデータから取り出せるデータ構造です。箱におもちゃを詰めていったとき、最初に入れたおもちゃは取り出せませんが、最後に入れたおもちゃは簡単に取り出せますよね。
スタックにデータを入れる操作をプッシュ(push)、取り出す操作をポップ(pop)と言います。
「データ1、データ2、データ3、データ4」という順番で入れたなら、取り出せる順番は逆で「データ4、データ3、データ2、データ1」となります。データ4より先に入れたものは最初に取り出せません。
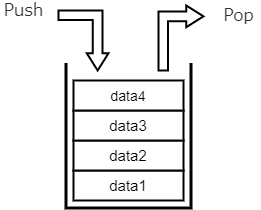
このように、最後に入れたものから取り出すという構造を後入れ先出し方式といい、英語だと「Last-In First-Out(LIFO)」と呼ばれます。キューと混合しないように注意しましょう。
メモ帳やエクセルなどの「操作を一つ戻す機能」などではスタックの構造が適していると言えます。
【C#】スタック型のデータにプッシュ・ホップするサンプル
C#では、複数のオブジェクトをスタックとして管理するコレクションが用意されています。実際にスタックにプッシュ・ホップしてみます。入れた順番と逆に取り出していることがわかります。一度取り出したものはスタックには残りません。
var stack = new Stack<string>();
stack.Push("あ");
stack.Push("い");
stack.Push("う");
stack.Push("え");
stack.Push("お");
string popResult = String.Empty;
while (stack.TryPop(out popResult))
{
Console.WriteLine(popResult);
}
//お
//え
//う
//い
//あツリー(木構造)
ツリーは、階層構造で親子関係を表すのに適しているデータ構造です。
最上階層のデータを親(root)、その下層にあるデータの分岐箇所を節(node)、最下層の分岐しないデータを葉(leaf)と言います。
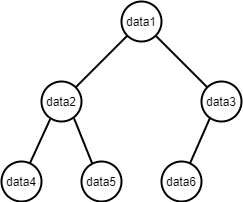
PCのディレクトリ階層と非常によく似ていますね。
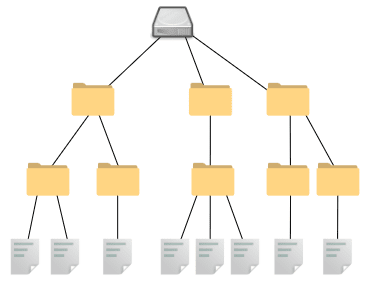
木構造をプログラムで表すには、「各データに親と子のアドレスを持たせる」方法と、「配列のインデックスを木構造に当てはめて管理する」方法がありますが、ここでは深くは触れません。
ツリー構造は細かく分けると数種類あるので、それぞれの特徴について触れていきます。
2分木
2分木は、節が最大2つの子を持てる木構造のことを言います。
2分探索木
2分探索木は、以下の条件を満たした二分木です。
- 節から分岐する左側の節は、親の節より値が小さい
- 節から分岐する右側の節は、親の節より値が大きい
ヒープ
ヒープは、以下の条件を満たした二分木です。
- 根に近い順に、節が左詰めになっている
- 親子関係の節が、決められた大小関係になっている。
大小関係が親>子の場合はrootが最大値になり、子>親の場合はrootが最小値になります。ヒープソートという整列アルゴリズムに用いれるデータ構造で、配列のインデックスで管理されることが多いです。


コメント