固定小数点と浮動小数点についてわかりやすく解説

２進数の小数点の表現方法について学んでみましょう。2進数の小数点の表現方法には「固定小数点数」と「浮動小数点数」の二種類があります。

固定小数点数は、決まった場所に小数点を置く数の表現方法のことで、

浮動小数点数は、指数を用いた数の表現方法のことです。

？？？

一言で説明するのはちょっと難しいので、具体的な計算方法を説明します。

固定小数点

固定小数点数は、小数点の位置を固定して表現する方式です。

「8ビットのうち頭6ビットを整数部にする」と決めたら、「111111.11」というような表現になりますし、「8ビットのうち頭3ビットを整数部にする」と決めたら、「111.11111」というような表現になります。

整数を表す場合には固定小数点数で「小数点の位置を一番右側にする」という表現にしているわけです。

浮動小数点数では、数を符号部、指数部、仮数部に分けて記憶する方式です。固定小数点数に比べて表現できる数の範囲が広いのが特徴です。数を以下のような式に整形してから、各要素を浮動小数点の形式に当てはめます。

\({符号}×{仮数}×2^{指数}\)

符号・・プラス、マイナスを表す
指数・・べき乗する値
仮数・・小数部分のこと
基数・・コンピュータでは2進数しか扱えないので2

そして、コンピュータ上ではこのような形式で保存します。

浮動小数点数の形式

これだけではパッとしないと思うので、実際に計算してみましょう。

実際のソフトウェアでも多用されている「IEEE754」形式について解説していきます。

IEEE754とは、浮動小数点数の形式の一つです。様々なコンピュータで共通の浮動小数点の計算を行うために作られた、国際的な規格となっています。

昔は各コンピュータメーカーで別々の形式が使われていて、いろいろと不便だから規格の統一化がされていったらしい

また、IEEE754には、数の大きさによって使い分けられるよう、二種類のバージョンが用意されています。

・単精度浮動小数点数：符号部1bit、指数部8bit、仮数部23bitの計32bit
・倍精度浮動小数点数：符号部1bit、指数部11bit、仮数部52bitの計64bit

今回は、10進数の「-10.25」を単精度浮動小数点数に変換してみましょう。

符号部Sを求めるにあたり、\({符号}={-1}^{S}\)という式が成り立ちますので、正のときは0、負のときは1となります。

10進数の「10.25」は2進数で「1010.01」と表すことができます。

→10進数から2進数への変換方法についてはこちらを参考にしてください。

IEEE754では、整数部の最小位が1になるように、
つまり、1.xxxという形になるように桁をずらし仮数と指数で表します。この作業のことを、正規化と言います。

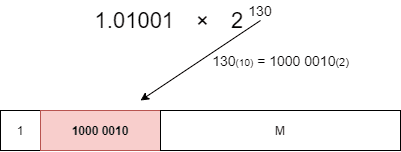
そのとおりに正規化をすると、\(1010.01={1.01001}×2^{3}\)となります。

IEEE754では、指数部を2の補数を使わず、正の値だけで表すという特徴があります。実際の値に127を加算することで、指数部を正の値だけで表すことが可能になります。(-127~128までを00000000~11111111で表せるようになります。)

このような加算する一定の値を、「バイアス値」、それを用いて数を表現することを「げたばき表現」と呼んだりします。

よって、指数部は3+127で130となり、それを2進数表記にすると10000010となります。

計算によって求められた指数部、仮数部と指数部を形式に当てはめます。仮数部においては、整数を省略して小数点のみを左詰めで当てはめます。

指数部をを当てはめて・・

仮数部を当てはめれば・・

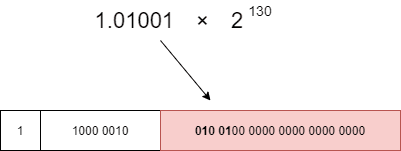
以上で完了となります。

浮動小数点数を手動で計算しなければいけないシーンなんてあまり無いと思いますが、ネット上にIEEE754変換器みたいなのがあるので興味があれば使ってみるのもいいでしょう。